一 试验研究结果

  　 钢筋混凝土梁从开始加荷直到破坏，可划分三个阶段：第Ⅰ 阶段，梁上没有裂缝，第Ⅰ 阶段末，裂缝即张出现；第Ⅱ阶段，梁带有裂缝工作，第Ⅱ阶段末，纵向钢筋屈服；第Ⅲ　阶段，裂缝急剧开展，到了第Ⅲ　阶段末，受压混凝土被压坏，整个梁也就破坏。

因此钢筋混凝土梁只有在荷载很小时，即在裂缝出现以前的第Ⅰ 阶段，挠度才能基本上与荷载成正比。到了第Ⅱ阶段，由于裂缝的出现，两者就不再成正比了。这是钢筋混凝土梁挠度变化规律的一个·重要特点，我们必须首先掌握。

二 钢筋混凝土梁开裂前的刚度

由位移计算公式（２-１）可见，EI越大，挠度就越小，梁的弯曲程度也越小（即曲率越小）。所以，梁的抗弯刚度（EI）是一个关键，它反映了梁低抗弯曲变形能力的大小。

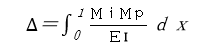
　                    　　　　　　　　　　                       （2-1）

式中Ｅ为材料的弹性模量，I为截面的惯性矩，乘积EI为截面的抗弯刚度；M_ｉ、M_p分别表示单位荷载和实际荷载作用时梁上任意截面的弯矩。M_ｉ、M_p与截面的抗弯刚度EI成反比。或者说，弯矩越大（梁弯曲得越厉害）；截面的抗弯刚度越大，曲率就越小（梁越不容易发生弯曲），这也是符合试验结果的。式中弹性模量Ｅ的单位为（N/mm^２），惯性矩I的单位为mm^４，故抗弯刚度EI的单位为（N-mm^２）。

对于钢筋混凝土梁，在裂缝出现以前（即第Ⅰ 阶段），刚度基本上是一个常数（E_CI₀），但是在第Ⅰ 阶段末，由于截面受拉区的混凝土已表现出弹塑性能，故实际的抗弯刚度比理想的弹性抗弯刚度要小。《钢筋混凝土结构设计规范》（GB 50010-2010）的（7.2.3）中式（7.2.3-2）规定，在计算位移时，对于使用阶段不出现裂缝的钢筋混凝土梁，应采用折减的抗弯刚度0.85 E_CI₀来计算，并用符号“B_s”表示，即：

            B_s=0.85 E_cI₀                          （2-2）

式中：0.85----刚度折减系数；

          E_c------混凝土的弹性模量；

          I₀------换算截面的惯性矩。

由于钢筋混凝土梁开裂前所能承受的荷载很小，而一般的构件在使用阶段均带有裂缝工作（无抗裂要求的工程），所以讨论钢筋混凝土梁开裂后的刚度计算更有实际意义。

三 钢筋混凝土梁在短期荷载作用下开裂后的刚度

      如上所述，在实际工程中多数的钢筋混凝土梁并无抗裂要求，正常使用时都已出现裂缝，梁处于第Ⅱ阶段。裂缝出现后，截面的刚度发生很大变化，在裂缝截面处，由于受拉区混凝土退出工作，截面大大削弱，换算截面惯性矩I₀以及刚度E_cI₀都随之减小；在每个裂缝之间的各截面，惯性矩I₀和刚度E_cI₀基本上仍同开裂前一样。于是沿梁的纵向，抗弯刚度B_s成为“木梳状”。

在第Ⅱ阶段的受力过程中，梁的刚度还会继续减小，一是由于少数新裂缝的出现，二是由于在已有裂缝的截面处，随裂缝的扩展，截面进一步削弱，换算截面的惯性矩I₀也继续减小，而受压区混凝土的塑性变形则有所发展，弹性模量E_c在降低，最后导致截面的刚度E_cI₀随荷载的增加而不断减小。显然，如把钢筋混凝土梁第Ⅱ阶段的刚度视作常数，并直接应用前面所述的梁的位移公式进行计算，是不正确的。

《钢筋混凝土结构设计规范》（GB 50010-2010）的（7.2.3）中式（7.2.3-1）规定，矩形、T形、到T形和I形截面，按裂缝控制等级要求的荷载组合作用下，钢筋混凝土受弯构件的短期刚度Bs，可按下式计算：

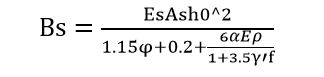
                 （3-1）

式中：φ----裂缝间纵向受拉普通钢筋应变不均匀系数，按本规范第7.1.2条确定；

          α_E----钢筋弹性模量与混凝土的弹性模量的比值，E_s/E_c；

          ρ----纵向受拉钢筋配筋率：对钢筋混凝土受弯构件，取为A_s/(bh₀)；

           A_s----混凝土构件配筋面积；

           h₀----梁截面的受压有效高度。

四 钢筋混凝土梁在长期荷载作用下的刚度

   公式（3-1）是钢筋混凝土梁在短期荷载作用下的刚度；试验表明，在长期荷载作用下，刚度还会降低。长期荷载作用下挠度增长的原因，主要是受压区混凝土徐变变形的发展；其次，在长期荷载作用下，混凝土与钢筋之间的粘结力有所破坏，受拉区混凝土继续退出工作，使裂缝与裂缝之间的钢筋的平均应变参数值有所增加。这些因素都使钢筋混凝土梁的钢筋降低，从而使挠度增加。

值得注意，在实际工程中，梁上既有恒载又有活载，恒载是长期作用的，而活荷载不是经常满载的，所有恒载对挠度的影响比活荷载要大得多。为了反映荷载长期作用对挠度的影响，规范中近似地将短期荷载作用下的刚度Bs予以折减，从而使所得的挠度能更符合长期荷载作用的实际情况。于是，钢筋混凝土梁在长期荷载作用下的刚度B为：

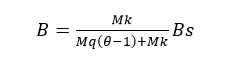
                                                   （4-1）

式中：M_k----按荷载的标准组合计算的弯矩，取计算区段内的最大弯矩值；

          M_q----按荷载的准永久组合计算的弯矩，取计算区段内的最大弯矩值；

    B_s----按荷载准永久组合计算的钢筋混凝土受弯构件；

    θ----考虑荷载长期作用对挠度增大的影响系数，按本规范第7.2.5条取用。

要提高梁的刚度，比较有效的方法是：增加截面的高度h；其次也可以用T形、工字形截面；或提高混凝土的强度等级等。

挠度值用下式计算：

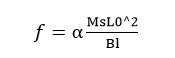
                            （4-2）

    也可以按工程力学中各类梁的内力计算公式中的挠度计算公式近似计算。

五 计算实例

1例：一矩形截面受弯构件，b×h=250×500mm，跨度L0=6500mm，混凝土强度C20，受拉钢筋4ф20Ⅱ级钢筋，保护层厚度c=25mm，承受荷载的长期效应组合作用的弯矩值M_q=95KN-m，荷载的短期效应组合作用的弯矩值M_k=120KN-m，求使用阶段跨中的挠度f。

1)基本参数

E_s=2.1×10⁵N/mm²,E_c=2.55×10⁴N/mm^2,，f_tk=1.5N/mm²

α_s=c+d/2=25+20/2=35mm,h₀=h-α_s=500-35=465mm

A_s=4π20²=1256mm²,ρ=A_S/bh₀=1256/250×465=0.0108

α_E=E_s/ E_c=2.1×10⁵/2.55×10⁴=8.24

2)求钢筋应变不均匀系数

A_te=0.5bh=0.5×250×500=62500mm²,ρ_te=As/A_te=1256/62500=0.0201

σ_ss=M_s/0.87h₀A_s=120×10⁶/0.87×465×236=236N/mm²

Ψ=1.1-(0.65f_tk/ρ_tkσ_ss)=1.1-(0.65×1.5/0.0201×236)=0.895

3)求短期刚度B_s

因构件无翼缘，故γ^’f=0，按公式（3-1）

B_s=(210000×1256×465²)/(1.15×0.895+0.2+6×8.24×0.0108)

=23.27×10¹²N-mm³

4)长期刚度

当受压纵向钢筋配筋率ρ^’=0时，θ=2.0，按（4-1）公式

B=(120×10⁶/(95×10⁶×(2-1)+120×10⁶)) ×32.37×10¹²=18.07×10¹²N-mm

5)求挠度f

按（4-2）公式，此处，α挠度系数，对均布荷载作用下的简支梁，α=5/48。

f=(5×120×10⁶×6500²)/(48×18.07×10¹²=29.23mm  <L/200满足要求

2 使用“钢筋混凝土结构辅助设计软件包 Beton V4.0”计算梁的挠度

1)用“钢筋混凝土结构辅助设计软件包 Beton V4.0”计算上面的例题，选取“钢筋混凝土结构辅助设计软件包 Beton V4.0”的“斜截面设计及极限状态验算”菜单项，如（图5-1）：

（图5-1）

打开“斜截面设计及极限状态验算”的窗口，输入上例数据，点击计算即可计算梁的挠度，见（图5-2）所示：

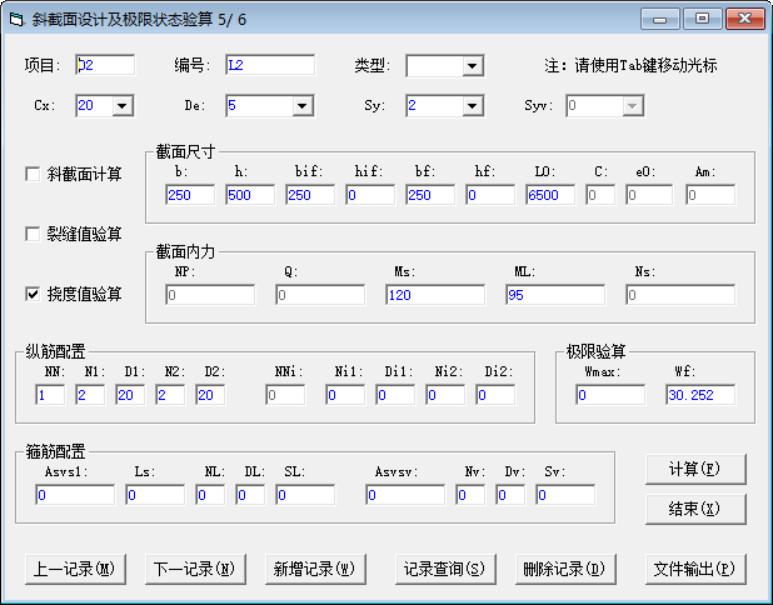
（图5-2）

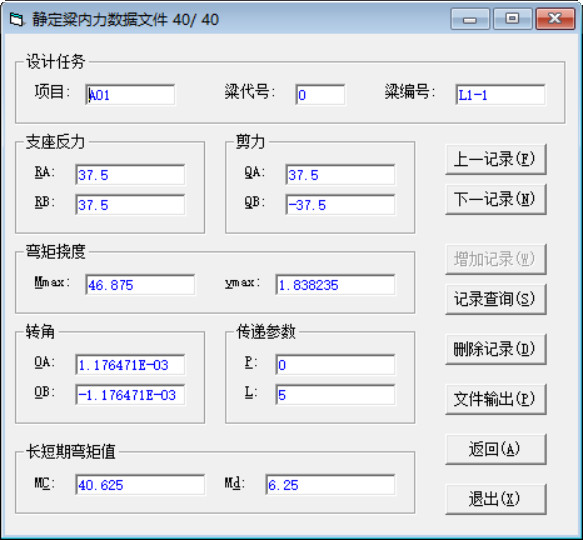
2)用梁内力计算程序模块来近似计算梁的挠度，选择菜单：“内力分析”—“静定梁荷载文件”，如（图5-3）。

（图5-3）

打开“静定梁荷载文件”窗口，如（图5-4）。

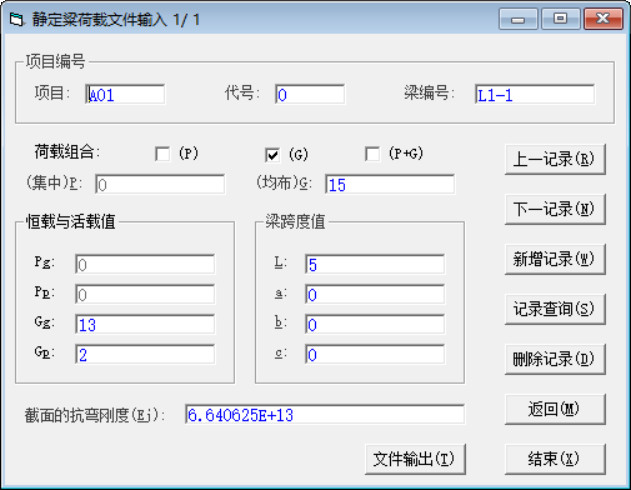
（图5-4）

本例是单跨静定梁，计算简图如（图5-5），梁上只作用均布荷载G=15KN-m，梁跨L=5米,混凝土强度等级为C20，矩形截面b×h=250×500，混凝土弹性模量E_c=2.55×10⁴N/mm^2,。矩形截面的惯性矩I₀按下式计算：

I₀=bh³/12=250×500³/12=2.604167×10⁹mm⁴

Ej=E_c×I₀=2.55×10⁴×2.083333E+09=6.640625×10¹³N-mm²

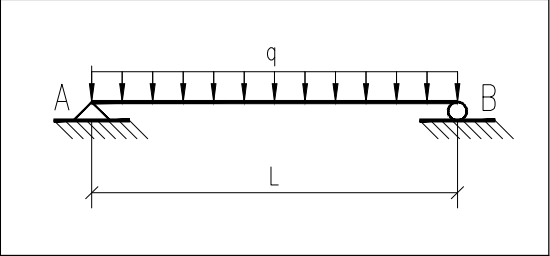
（图5-5）

均布荷载作用下单跨静定梁的挠度公式：

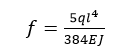
                   （5-1）

（图5-6）

（完）

2021年12月5日